C: Multidimensional Arrays

Consider a tabular data, such as the matrix below

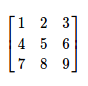
The elements of the above matrix can be grouped row wise into one-dimensional arrays: {1,2,3}, {4,5,6} and {7,8,9}. We further create another array consisting of the above one-dimensional arrays as its elements


{ {1,2,3}, {4,5,6}, {7,8,9} };

Such an array of one-dimensional arrays forms a two-dimensional (2D) array.

The number of elements in a two-dimensional array gives its row dimension and the number of elements in each one-dimensional array gives its column dimension. A two-dimensional array of i rows and j columns of type int is declared as


int n[i][j]; // [rows][columns]

A two-dimensional array of 2 rows and 3 columns is declared and initialized as


int n[2][3] = { {1,2,3}, {4,5,6} }; // 2 rows, 3 columns

Its element at i^th row and j^th column is given by n[i][j] (the subscripts/indexes start from 0). So, n[0][0] refers to the element at first row and first column, which is 1. n[1][0] refers to the element at second row and first column, which is 4.

For two-dimensional arrays, specifying the number of rows is not compulsory. So the below declaration and initialization works just fine


int n[][3] = { {1,2,3}, {4,5,6} }; // 2 rows, 3 columns

However, the second dimension (number of columns) has to be specified. Without it, the array declaration itself becomes invalid and an error will be thrown during compilation: "array type has incomplete element type."

Print Elements of a Two Dimensional (2D) Array

Here we traverse and print the elements of the above initialized two-dimensional (2D) array n


#include <stdio.h>

main() {
	int n[2][3] = { {1,2,3}, {4,5,6} }; // array of 2 rows and 3 columns
	unsigned i, j;
	for(i = 0;i < 2; i++) { // looping the row
		for(j = 0;j < 3; j++) { // looping the column
			printf("%d ", n[i][j]);
		}
		printf("\n");
	}
}

Two dimensional arrays are largely used in matrix computations.

Three Dimensional (3D) Arrays

We will illustrate three dimensional (3D) arrays with the coordinates of two tetrahedrons. A tetrahedron is a polyhedron made up of 4 vertices, 6 edges, and 4 triangular faces. Consider a tetrahedron with vertices having the coordinates: (1, 1, 1), (−1, −1, 1), (−1, 1, −1), (1, −1, −1).

Generated by Gnuplot

These coordinates can be stored in a two-dimensional (2D) array of 4 rows and 3 columns as


int n[4][3] = 
	{	
		{1,1,1},
		{-1,-1,1},
		{-1,1,-1},
		{1,-1,-1}		
	};

Now consider another tetrahedron with coordinates: (-1,1,1), (1,-1,1), (1,1,-1), (-1,-1,-1). Storing these two sets of coordinates will require creating another dimension of size 2 for the existing array as shown below


int n[2][4][3] = 
	{
		{
			{1,1,1},
			{-1,-1,1},
			{-1,1,-1},
			{1,-1,-1}
		},
		{
			{-1,1,1},
			{1,-1,1},
			{1,1,-1},
			{-1,-1,-1}
		}	
	};

The above array is a three-dimensional (3D) array. The below program prints the coordinates of the vertices of the two tetrahedrons as two separate matrices


int n[2][4][3] =  // array of 3 dimensions
	{ 
		{
			{1,1,1}, 
			{-1,-1,1},
			{-1,2,-1},
			{1,-1,-1}
		},
		{
			{-1,1,1},
			{1,-1,1},
			{1,1,-1},
			{-1,-1,-1}
		}
	}; 

unsigned i, j, k;
for(i = 0;i < 2; i++) { // looping through the first dimension
	for(j = 0;j < 4; j++) { // looping through the second dimension
		for(k = 0;k < 3;k++) { // looping through the third dimension
			printf("%d ", n[i][j][k]);
		}
		printf("\n");
	}
	printf("----- \n");
}