NumPy: Matrix Multiplication

In this tutorial, we will learn how to find the product of two matrices in Python using a function called numpy.matmul(), which belongs to its scientfic computation package NumPy.

A product of an $m \times p$ matrix $A = [a_{ij}]$ and an $p \times n$ matrix $B = [b_{ij}]$ results in an $m \times n$ matrix $C = [c_{ij}]$ where

$$ c_{ij} = a_{i1}b_{1j} + a_{i2}b_{2j} + ... + a_{ip}b_{pj} $$

and the indices $i = (1,2, ... ,m)$ and $j = (1,2, ... ,n)$.

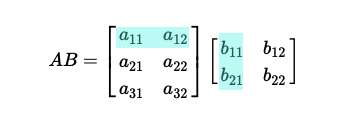
The product of two matrices $A$ and $B$ in the order $AB$ is written expicitly as

$$ AB = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{bmatrix} \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix} $$

We bring to mind again that matrix multiplication operation is row to column, so each element of a particular row in the first matrix is multiplied into the corresponding element of the column in the second matrix, which are then summed together.

We note that multiplication between two matrices $A$ and $B$ is defined in the order $AB$ if and only if the number of columns of the matrix $A$ is equal to the number of rows of the matrix $B$. If $AB$ is defined, then

$$ AB = \begin{bmatrix} a_{11}b_{11} + a_{12}b_{21} & a_{11}b_{12} + a_{12}b_{22} \\ a_{21}b_{11} + a_{22}b_{21} & a_{21}b_{12} + a_{22}b_{22} \\ a_{31}b_{11} + a_{32}b_{21} & a_{31}b_{12} + a_{32}b_{22} \end{bmatrix} $$

We pick an example from a Schaum's Outline Series book Theory and Problems of Matrices by Frank Aryes, Jr¹. $A$ is a $3 \times 3$ matrix

$$ A = \begin{bmatrix} 2 & 1 & 0 \\ 3 & 2 & 0 \\ 1 & 0 & 1 \end{bmatrix} $$

and $B$ is a $3 \times 4$ matrix

$$ B = \begin{bmatrix} 1 & 1 & 1 & 0\\ 2 & 1 & 1 & 0\\ 2 & 3 & 1 & 2 \end{bmatrix} $$

Since the number of columns of matrix $A$ is equal to the number of rows of matrix $B$, the product $AB$ is defined. The result will be a $3 \times 4$ matrix.

To find $AB$, which is

$$ \begin{bmatrix} 2 & 1 & 0 \\ 3 & 2 & 0 \\ 1 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 1 & 1 & 0\\ 2 & 1 & 1 & 0\\ 2 & 3 & 1 & 2 \end{bmatrix} $$

we make use of NumPy's numpy.matmul() function.

But before you use it, you first need to check the version of NumPy installed in your system. The following code snippet will print your NumPy's version.

				
					import numpy as np
					print(np.version.version)
				
			

If it is below 1.10, it will not run. Upgrade to the latest version.

The code for computing $AB$ in NumPy is

				
					import numpy as np

					a = np.array([[2, 1, 0], [3, 2, 0], [1, 0, 1]])
					b = np.array([[1, 1, 1, 0], [2, 1, 1, 0], [2, 3, 1, 2]])

					c = np.matmul(a,b)

					print(c)
				
			

If you run the script, you will get a $3 \times 4$ matrix as

				
					[[4 3 3 0]
					 [7 5 5 0]
					 [3 4 2 2]]