Python Program: Factorial of a Number

The factorial of a given positive integer $n$ is defined as the product of all integers from $n$ down to 1.

The factorial of $n$ is denoted by $n!$

$n! = n\times(n-1)\times ... \times1$

For example,

$4! = 4\times3\times2\times1 = 24$

We calculate factorials only of positive integers and 0, or whole numbers. Factorials of negative numbers are undefined. Also, note that $0! = 1$.

Below is the Python program to compute the factorial of a given number $n$. Here, $n$ is pre-assigned the value $7$, so we basically are computing $7!$

				
					n = 7
					factorial = 1

					if n < 0:
					   print("Factorial is not defined for -ve numbers")
					elif n == 0:
					   print(n, "! = ", 1)
					else:
					   for i in range(1,n + 1):
					       factorial = factorial*i
					   print(n ,"! = ", factorial)
				
			

Upon execution, the above program gives the factorial of $7$ as

				
					7! = 5040
				
			

We will now modify the above Python code to accept $n$ dynamically; we replace the top line of code where $n$ was previously pre-assigned with some value with int(input("n = ")).

				
					n = int(input("n = "))
					factorial = 1

					# check if the number is negative, positive or zero
					if n < 0:
					   print("Factorial is not defined for -ve numbers")
					elif n == 0:
					   print(n, "! = ", 1)
					else:
					   for i in range(1,n + 1):
					       factorial = factorial*i
					   print(n ,"! = ", factorial)
				
			

On running the program, the prompt to enter a value of $n$ appears.

				
					n = 
				
			

And then you enter some value for $n$ and it gives its computed factorial.

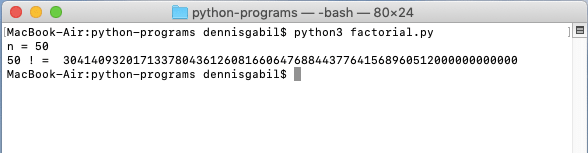
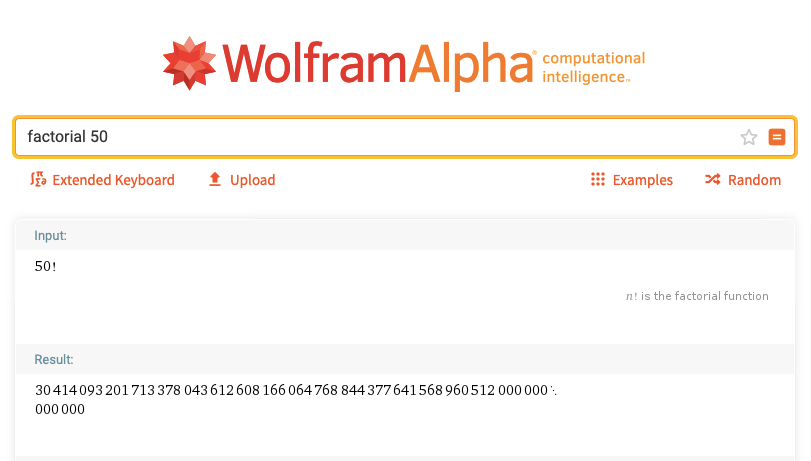
Now there exists a powerful math engine called Wolfram Alpha, designed by Stephen Wolfram, which you can use to cross-check the values of factorial of bigger numbers.

Here we compute the factorial of 50 using Wolfram Alpha online.

					
						def factorial(m):
						   if m == 1:
						       return m
						   else:
						       return m*factorial(m-1)

						n = int(input("n = "))

						if n < 0:
						   print("Factorial is not defined for -ve numbers")
						elif n == 0:
						   print(n, "! = ", 1)
						else:
						   print(n ,"! = ", factorial(n))
					
				

					
						n = 12
						12 ! =  479001600