Permutation (nPr) and Combination (nCr) in C

Permutation is the number of ways an ordered subset can be obtained of $r$ elements from a set of $n$ elements.

The below example illustrates the number of ways in which three different circles (red, yellow and black) can be permutated, taken two at a time. It is 6.

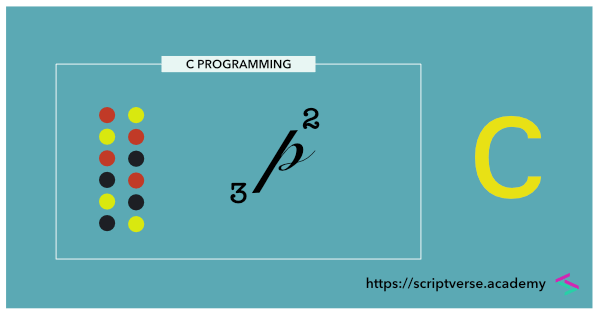
c program permutation

The permutation of $n$ things taken $r$ at a time is denoted by $_{n} \text{P}^{r}$ and the formula for obtaining it is

$_{n} \text{P}^{r} = \frac{n!}{(n-r)!}$

Below we write a C program to compute the permutation of $n$ things taken $r$ at a time, based on the above formula. A little note to be taken here, your input should be $r \leq n$. 

				
				#include <stdio.h>

				unsigned long nPr(unsigned short n, unsigned short r);
				unsigned long factorial(unsigned short int);

				int main() {
					unsigned short int n, r;

					printf("Enter n: ");
					scanf("%hu", &n);


					printf("Enter r: ");
					scanf("%hu", &r);

					printf("%huP%hu: %lu", n, r, nPr(n,r));
					printf("\n");

					return 0;
				}

				unsigned long nPr(unsigned short n, unsigned short r) {
					return factorial(n)/factorial(n-r); 
				}

				unsigned long factorial(unsigned short n) {
					unsigned long f;
					
					if(n == 0 || n == 1)
						return 1;
					else 
						f = n * factorial(n-1);

					return f;
				}

We run the program for $n = 6$ and $r = 2$ 

				
					$ ./a.out
					Enter n: 6
					Enter r: 2

It outputs: 

				
					6P2: 30

When order is not considered, it becomes a combination. The below example illustrates the number of ways in which three different circles (red, yellow and black) can be combined, taken two at a time. It is 3.

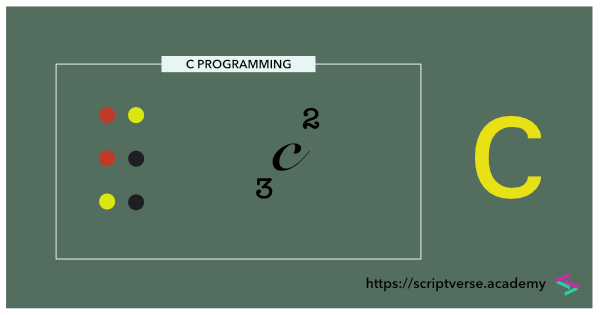
c program combination

The combination of $n$ things taken $r$ at a time is denoted by $_{n} \text{C}^{r}$ and the formula for obtaining it is

$_{n} \text{C}^{r} = \frac{n!}{r!(n-r)!}$

It is also known as the Binomial Coefficient. Below is the C program based on the above formula. 

				
				#include <stdio.h>

				unsigned long nCr(unsigned short n, unsigned short r);
				unsigned long factorial(unsigned short int);

				int main() {
					unsigned short int n, r;

					printf("Enter n: ");
					scanf("%hu", &n);


					printf("Enter r: ");
					scanf("%hu", &r);

					printf("%huC%hu: %lu", n, r, nCr(n,r));
					printf("\n");

					return 0;
				}

				unsigned long nCr(unsigned short n, unsigned short r) {
					return factorial(n)/(factorial(r)*factorial(n-r)); 
				}

				unsigned long factorial(unsigned short n) {
					unsigned long f;
					
					if(n == 0 || n == 1)
						return 1;
					else 
						f = n * factorial(n-1);

					return f;
				}

We execute the above program for $n = 10$ and $r = 6$ 

				
					$ ./a.out
					Enter n: 10
					Enter r: 6

And we get the output: 

				
					10C6: 210