Python Program: GCD/HCF

The Greatest Common Divisor (GCD) of two integers $a$ and $b$, with one of them non-zero, is the largest integer which divides both $a$ and $b$ completely. For example, the GCD of 12 and 18 is 6. GCD is also known as the Highest Common Factor (HCF).

The GCD can also be defined for three or more integers as the largest integer that divides them all. Here, we will write a simple program in Python to compute the GCD of two integers.

We define a recursive function gcd() which takes two integer arguments and return their GCD.

				
				def gcd(a, b):
				    if b > a:
				        return gcd(b, a)
				    if a % b == 0:
				        return b
				    return gcd(b, a % b) 
				
			

The full program using the above recursive function is implemented below with the provision to take two integer inputs and display their GCD.

				
				a = int(input("First number = "))
				b = int(input("Second number = "))

				def gcd(a, b):
				    if b > a:
				        return gcd(b, a)
				    if a % b == 0:
				        return b
				    return gcd(b, a % b) 

				print("GCD/HCF of", a, "and" , b, "is", gcd(a,b))
				print()
				
			

We run the above program and find the GCD of $84$ and $123$. It gives the value $3$.

Using math.gcd()

The Python math module actually has the gcd() function which computes the GCD/HCF of two integers $a$ and $b$.

						
						import math 

						a = int(input("First number = "))
						b = int(input("Second number = "))

						print("GCD/HCF of", a, "and", b, "is", math.gcd(a,b))
						print()
						
					

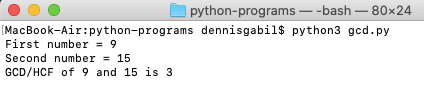
Below we compute the GCD of $9$ and $15$ using the gcd() function of the math module and get the value as $3$.