Matplotlib: Plot a Function y=f(x)

In our previous tutorial, we learned how to plot a straight line, or linear equations of type $y=mx+c$.

Here, we will be learning how to plot a defined function $y=f(x)$ in Python, over a specified interval.

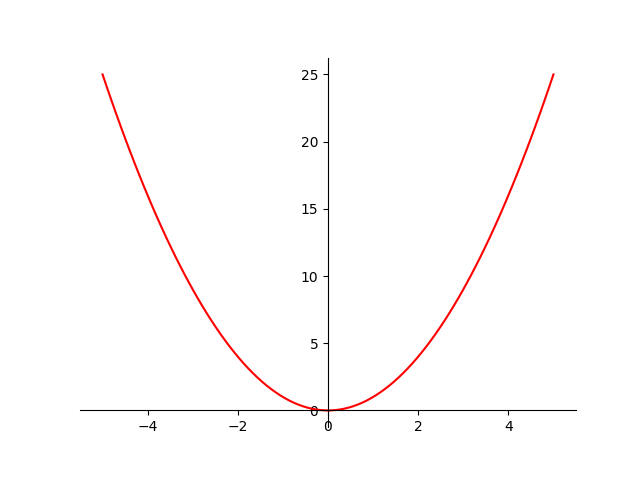
We start off by plotting the simplest quadratic equation $y=x^{2}$.

Quadratic Equation

Quadratic equations are second order polynomial equations of type $ax^{2} + bx + c = 0$, where $x$ is a variable and $a \ne 0$. Plotting a quadratic function is almost the same as plotting the straight line in the previous tutorial.

Below is the Matplotlib code to plot the function $y=x^{2}$. It is a simple straight-forward code; the bulk of it in the middle is for setting the axes. As the exponent of $x$ is $2$, there will only be positive values of $y$, so we can position ax.spines['bottom'] at the bottom. 

					
						import matplotlib.pyplot as plt
						import numpy as np

						# 100 linearly spaced numbers
						x = np.linspace(-5,5,100) 

						# the function, which is y = x^2 here
						y = x**2

						# setting the axes at the centre
						fig = plt.figure()
						ax = fig.add_subplot(1, 1, 1)
						ax.spines['left'].set_position('center')
						ax.spines['bottom'].set_position('zero')
						ax.spines['right'].set_color('none')
						ax.spines['top'].set_color('none')
						ax.xaxis.set_ticks_position('bottom')
						ax.yaxis.set_ticks_position('left')

						# plot the function
						plt.plot(x,y, 'r') 

						# show the plot
						plt.show()
matplotlib quadratic equation

Cubic Equation

Next, we will plot the simplest cubic function $y=x^{3}$.

Since the exponent in $y=x^{3}$ is $3$, the power is bound to have negative values for negative values of $x$. Therefore, for visibility of negative values in the $y$-axis, we need to move the $x$-axis to the centre of the graph. ax.spines['bottom'] is thus positioned to centre. 

					
						import matplotlib.pyplot as plt
						import numpy as np

						# 100 linearly spaced numbers
						x = np.linspace(-5,5,100) 

						# the function, which is y = x^3 here
						y = x**3

						# setting the axes at the centre
						fig = plt.figure()
						ax = fig.add_subplot(1, 1, 1)
						ax.spines['left'].set_position('center')
						ax.spines['bottom'].set_position('center')
						ax.spines['right'].set_color('none')
						ax.spines['top'].set_color('none')
						ax.xaxis.set_ticks_position('bottom')
						ax.yaxis.set_ticks_position('left')

						# plot the function
						plt.plot(x,y, 'g') 

						# show the plot
						plt.show()
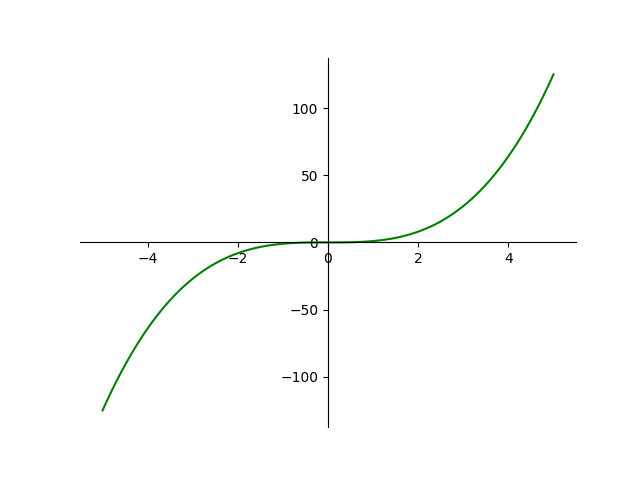
matplotlib cubic equation

Trigonometric Functions

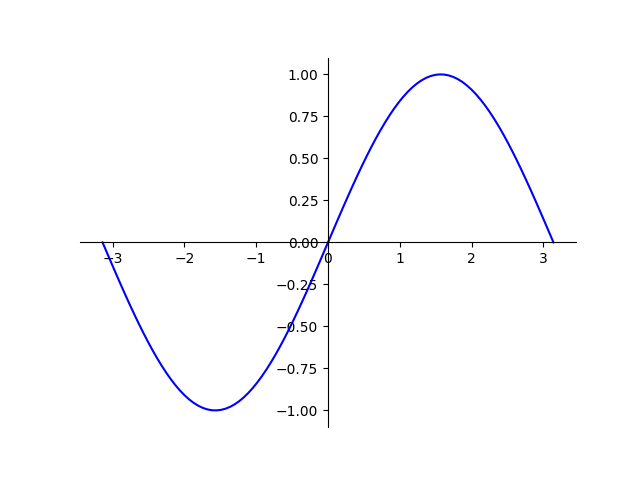
Here we plot the trigonometric function $y=\text{sin}(x)$ for the values of $x$ between $-\pi$ and $\pi$. The linspace() method has its interval set from $-\pi$ to $\pi$. 

					
					import matplotlib.pyplot as plt
					import numpy as np

					# 100 linearly spaced numbers
					x = np.linspace(-np.pi,np.pi,100)

					# the function, which is y = sin(x) here
					y = np.sin(x)

					# setting the axes at the centre
					fig = plt.figure()
					ax = fig.add_subplot(1, 1, 1)
					ax.spines['left'].set_position('center')
					ax.spines['bottom'].set_position('center')
					ax.spines['right'].set_color('none')
					ax.spines['top'].set_color('none')
					ax.xaxis.set_ticks_position('bottom')
					ax.yaxis.set_ticks_position('left')

					# plot the function
					plt.plot(x,y, 'b')

					# show the plot
					plt.show()
matplotlib sinx

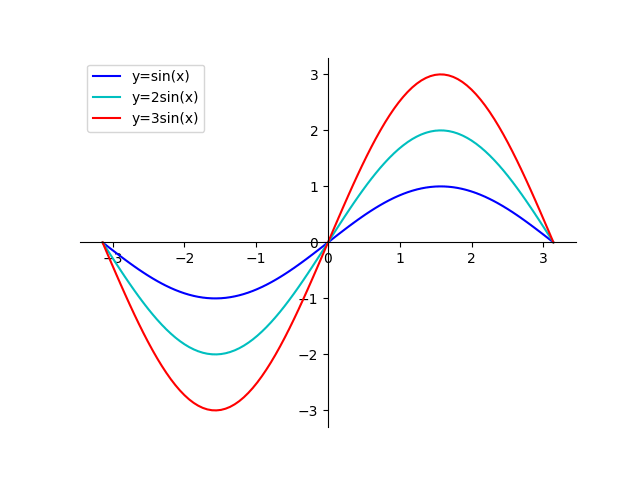
Let us plot it together with two more functions, $y=2\text{sin}(x)$ and $y=3\text{sin}(x)$. This time, we label the functions. 

					
					import matplotlib.pyplot as plt
					import numpy as np

					# 100 linearly spaced numbers
					x = np.linspace(-np.pi,np.pi,100)

					# the function, which is y = sin(x) here
					y = np.sin(x)

					# setting the axes at the centre
					fig = plt.figure()
					ax = fig.add_subplot(1, 1, 1)
					ax.spines['left'].set_position('center')
					ax.spines['bottom'].set_position('center')
					ax.spines['right'].set_color('none')
					ax.spines['top'].set_color('none')
					ax.xaxis.set_ticks_position('bottom')
					ax.yaxis.set_ticks_position('left')

					# plot the functions
					plt.plot(x,y, 'b', label='y=sin(x)')
					plt.plot(x,2*y, 'c', label='y=2sin(x)')
					plt.plot(x,3*y, 'r', label='y=3sin(x)')

					plt.legend(loc='upper left')

					# show the plot
					plt.show()
matplotlib sinx multiple

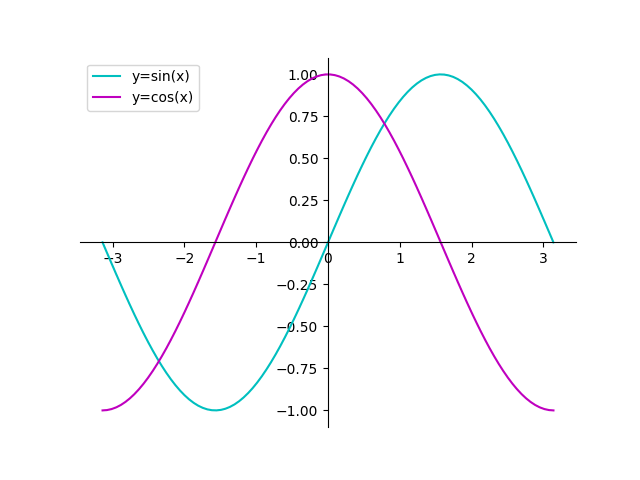
And here we plot together both $y=\text{sin}(x)$ and $y=\text{cos}(x)$ over the same interval $-\pi$ to $\pi$. 

					
					import matplotlib.pyplot as plt
					import numpy as np

					# 100 linearly spaced numbers
					x = np.linspace(-np.pi,np.pi,100)

					# the functions, which are y = sin(x) and z = cos(x) here
					y = np.sin(x)
					z = np.cos(x)

					# setting the axes at the centre
					fig = plt.figure()
					ax = fig.add_subplot(1, 1, 1)
					ax.spines['left'].set_position('center')
					ax.spines['bottom'].set_position('center')
					ax.spines['right'].set_color('none')
					ax.spines['top'].set_color('none')
					ax.xaxis.set_ticks_position('bottom')
					ax.yaxis.set_ticks_position('left')

					# plot the functions
					plt.plot(x,y, 'c', label='y=sin(x)')
					plt.plot(x,z, 'm', label='y=cos(x)')

					plt.legend(loc='upper left')

					# show the plot
					plt.show()
matplotlib sinx cosx

Exponential Function

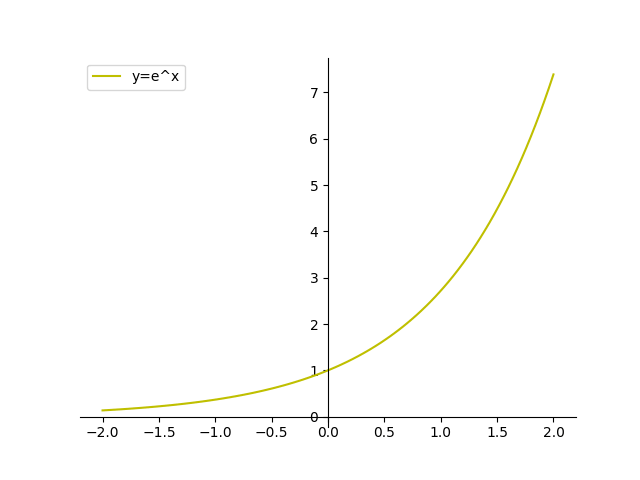
The exponential function $y=e^{x}$ is never going to have any negative values for any value of $x$. So we move the $x$-axis to the bottom again by setting ax.spines['bottom'] to zero. We plot it over the interval $-2$ to $2$. 

					
						import matplotlib.pyplot as plt
						import numpy as np

						# 100 linearly spaced numbers
						x = np.linspace(-2,2,100)

						# the function, which is y = e^x here
						y = np.exp(x)

						# setting the axes at the centre
						fig = plt.figure()
						ax = fig.add_subplot(1, 1, 1)
						ax.spines['left'].set_position('center')
						ax.spines['bottom'].set_position('zero')
						ax.spines['right'].set_color('none')
						ax.spines['top'].set_color('none')
						ax.xaxis.set_ticks_position('bottom')
						ax.yaxis.set_ticks_position('left')

						# plot the function
						plt.plot(x,y, 'y', label='y=e^x')
						plt.legend(loc='upper left')

						# show the plot
						plt.show()
matplotlib expx